These is the beginning of my writeups for the CryptoHack challenges. I will be starting with the Modular Math challenges.
Quadratic Residues
We need to do simple brute force on all the values in the field as prime p is very small. We can use the following code to solve the challenge.
1
2
3
4
5
6
7
8
9
p = 29
ints = [14, 6, 11]
flag = 100000 # max
for n in ints:
for a in range(1,29):
if pow(a,2,p) == n:
flag = min(flag,a)
print(flag)
# Answer: 8
Legendre Symbol
We have to divide this problem into two part. First find the quadratic residue from the given ints list and then find the square root of the quadratic residue. Given that p = 3 (mod 4), we can show that the square root of a quadratic residue is given by pow(a, (p+1)//4, p). This is the link to the proof.
Basically we do the following thing 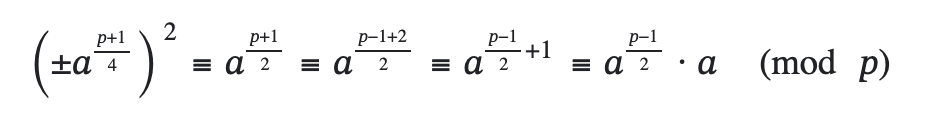
here a ^ (p-1)/2 is congruent to 1 (mod p) as p is prime a ^ (p+1)/4 is the square root of a.
1
2
3
4
5
6
7
8
9
10
11
p = 101524035174539890485408575671085261788758965189060164484385690801466167356667036677932998889725476582421738788500738738503134356158197247473850273565349249573867251280253564698939768700489401960767007716413932851838937641880157263936985954881657889497583485535527613578457628399173971810541670838543309159139
ints = [25081841204695904475894082974192007718642931811040324543182130088804239047149283334700530600468528298920930150221871666297194395061462592781551275161695411167049544771049769000895119729307495913024360169904315078028798025169985966732789207320203861858234048872508633514498384390497048416012928086480326832803, 45471765180330439060504647480621449634904192839383897212809808339619841633826534856109999027962620381874878086991125854247108359699799913776917227058286090426484548349388138935504299609200377899052716663351188664096302672712078508601311725863678223874157861163196340391008634419348573975841578359355931590555, 17364140182001694956465593533200623738590196990236340894554145562517924989208719245429557645254953527658049246737589538280332010533027062477684237933221198639948938784244510469138826808187365678322547992099715229218615475923754896960363138890331502811292427146595752813297603265829581292183917027983351121325, 14388109104985808487337749876058284426747816961971581447380608277949200244660381570568531129775053684256071819837294436069133592772543582735985855506250660938574234958754211349215293281645205354069970790155237033436065434572020652955666855773232074749487007626050323967496732359278657193580493324467258802863, 4379499308310772821004090447650785095356643590411706358119239166662089428685562719233435615196994728767593223519226235062647670077854687031681041462632566890129595506430188602238753450337691441293042716909901692570971955078924699306873191983953501093343423248482960643055943413031768521782634679536276233318, 85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771, 50576597458517451578431293746926099486388286246142012476814190030935689430726042810458344828563913001012415702876199708216875020997112089693759638454900092580746638631062117961876611545851157613835724635005253792316142379239047654392970415343694657580353333217547079551304961116837545648785312490665576832987, 96868738830341112368094632337476840272563704408573054404213766500407517251810212494515862176356916912627172280446141202661640191237336568731069327906100896178776245311689857997012187599140875912026589672629935267844696976980890380730867520071059572350667913710344648377601017758188404474812654737363275994871, 4881261656846638800623549662943393234361061827128610120046315649707078244180313661063004390750821317096754282796876479695558644108492317407662131441224257537276274962372021273583478509416358764706098471849536036184924640593888902859441388472856822541452041181244337124767666161645827145408781917658423571721, 18237936726367556664171427575475596460727369368246286138804284742124256700367133250078608537129877968287885457417957868580553371999414227484737603688992620953200143688061024092623556471053006464123205133894607923801371986027458274343737860395496260538663183193877539815179246700525865152165600985105257601565]
a = 0
for i in ints:
if pow(i,(p-1)//2,p) == 1:
a = i
break
print(pow(a,(p+1)//4,p))
Modular Square Root
In the problem Legendre Symbol we have already found the square root of the quadratic residue for the prime where p satisfies the condition p = 3 (mod 4). We now need to similarly handle the case where p can also be p = 1 (mod 4).
- Sage Math have a built in function to find the square root of a quadratic residue. We can use the following code to solve the challenge.
Chinese Remainder Theorem
The given question is a simple application of the Chinese Remainder Theorem. To solve this programatically we will be using Gauss algorithm to find the value of x.
- Gauss Algorithm
1 2 3 4 5 6 7 8 9 10 11
def ChineseRemainderGauss(n,N,a): # n is the list of moduli # N is the product of all moduli # a is the list of remainders # x is the solution x = 0 for i in range(len(n)): ai = a[i] ni = N//n[i] x += ai * ni * invmod(bi,n[i]) return x%N
- Function to find iverse modulo of a number (Extended Euclidean Algorithm).
1 2 3 4 5 6 7
def invmod(x, y): x0, x1, y0, y1 = 1, 0, 0, 1 while y > 0: q, x, y = math.floor(x / y), y, x % y x0, x1 = x1, x0 - q * x1 y0, y1 = y1, y0 - q * y1 return x0 % y
Adrien’s Signs
This challenge does not introduce any new concept and can be solved using concpets learnt in previous chals. We have been given a script source.py which is used to encode the flag.
Interpreting source.py
We iterate through each char of the flag and convert the ASCII value to binary string of size 8 and append them in a string plaintext. Then for corresponding to each bit we generate a random n and append it in the list if bit is 1 or else we append -n % p. The resulting list is provided as output.txt. We have to find a way to get back the binary string plaintext then we can extract the flag from it.
compute p % 4 it will result into 3. Hence p is of type 3 (mod 4). So if the value of pow(x,(p-1)//2,p) == 1 then the corresponding bit will 1 else 0. Because when we do the above for -n%p it will give pow(x,(p-1)//2,p) == -1.
Here is the code for this chal.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
encFlag = [67594220461269, 501237540280788, 718316769824518, 296304224247167, 48290626940198, 30829701196032, 521453693392074, 840985324383794, 770420008897119, 745131486581197, 729163531979577, 334563813238599, 289746215495432, 538664937794468, 894085795317163, 983410189487558, 863330928724430, 996272871140947, 352175210511707, 306237700811584, 631393408838583, 589243747914057, 538776819034934, 365364592128161, 454970171810424, 986711310037393, 657756453404881, 388329936724352, 90991447679370, 714742162831112, 62293519842555, 653941126489711, 448552658212336, 970169071154259, 339472870407614, 406225588145372, 205721593331090, 926225022409823, 904451547059845, 789074084078342, 886420071481685, 796827329208633, 433047156347276, 21271315846750, 719248860593631, 534059295222748, 879864647580512, 918055794962142, 635545050939893, 319549343320339, 93008646178282, 926080110625306, 385476640825005, 483740420173050, 866208659796189, 883359067574584, 913405110264883, 898864873510337, 208598541987988, 23412800024088, 911541450703474, 57446699305445, 513296484586451, 180356843554043, 756391301483653, 823695939808936, 452898981558365, 383286682802447, 381394258915860, 385482809649632, 357950424436020, 212891024562585, 906036654538589, 706766032862393, 500658491083279, 134746243085697, 240386541491998, 850341345692155, 826490944132718, 329513332018620, 41046816597282, 396581286424992, 488863267297267, 92023040998362, 529684488438507, 925328511390026, 524897846090435, 413156582909097, 840524616502482, 325719016994120, 402494835113608, 145033960690364, 43932113323388, 683561775499473, 434510534220939, 92584300328516, 763767269974656, 289837041593468, 11468527450938, 628247946152943, 8844724571683, 813851806959975, 72001988637120, 875394575395153, 70667866716476, 75304931994100, 226809172374264, 767059176444181, 45462007920789, 472607315695803, 325973946551448, 64200767729194, 534886246409921, 950408390792175, 492288777130394, 226746605380806, 944479111810431, 776057001143579, 658971626589122, 231918349590349, 699710172246548, 122457405264610, 643115611310737, 999072890586878, 203230862786955, 348112034218733, 240143417330886, 927148962961842, 661569511006072, 190334725550806, 763365444730995, 516228913786395, 846501182194443, 741210200995504, 511935604454925, 687689993302203, 631038090127480, 961606522916414, 138550017953034, 932105540686829, 215285284639233, 772628158955819, 496858298527292, 730971468815108, 896733219370353, 967083685727881, 607660822695530, 650953466617730, 133773994258132, 623283311953090, 436380836970128, 237114930094468, 115451711811481, 674593269112948, 140400921371770, 659335660634071, 536749311958781, 854645598266824, 303305169095255, 91430489108219, 573739385205188, 400604977158702, 728593782212529, 807432219147040, 893541884126828, 183964371201281, 422680633277230, 218817645778789, 313025293025224, 657253930848472, 747562211812373, 83456701182914, 470417289614736, 641146659305859, 468130225316006, 46960547227850, 875638267674897, 662661765336441, 186533085001285, 743250648436106, 451414956181714, 527954145201673, 922589993405001, 242119479617901, 865476357142231, 988987578447349, 430198555146088, 477890180119931, 844464003254807, 503374203275928, 775374254241792, 346653210679737, 789242808338116, 48503976498612, 604300186163323, 475930096252359, 860836853339514, 994513691290102, 591343659366796, 944852018048514, 82396968629164, 152776642436549, 916070996204621, 305574094667054, 981194179562189, 126174175810273, 55636640522694, 44670495393401, 74724541586529, 988608465654705, 870533906709633, 374564052429787, 486493568142979, 469485372072295, 221153171135022, 289713227465073, 952450431038075, 107298466441025, 938262809228861, 253919870663003, 835790485199226, 655456538877798, 595464842927075, 191621819564547]
flag = ""
a = 288260533169915
p = 1007621497415251
for ch in encFlag:
if pow(ch,(p-1)//2,p)==1:
flag += '1'
else:
flag += '0'
flag
ls = [chr(int(flag[i:i+8],2)) for i in range(0,len(flag),8)]
result = ""
for i in ls:
result += i
print(result)